القيمة الفعالة للتيار المتردد RMS

كم مرة استخدمت مصطلح RMS أثناء التعامل مع دوائر التيار المتردد؟ حسنًا، لا يمكنك إحصاء هذا العدد، لأننا نستخدمه كل يوم تقريبًا.

الجهد الذي يغذي منازلنا هو قيمة فعالة. الفولتية لأنظمة النقل والتوزيع مثل220V ،11kV ،36kV… هي أيضًا قيم فعالة.

تعتبر القيمة الفعالة للتيار المتردد مصطلحًا مهمًا في الكهرباء وموجود في كل مكان تقريبًا في الهندسة الكهربائية. لذلك، يجب أن يعرف كل مهندس كهربائي مفهوم القيمة الفعالة .

ولكن، ما مفهوم القيمة الفعالة للتيار المتردد RMS؟ ولماذا هي مهمة جدًا؟‌‌ تشرح هذه المقالة مفهوم نظرية القيمة الفعالة “Root Mean Square Value” وأهميتها وكيفية حسابها مع مثال محلول.

حساب القدرة الكهربائية في التيار المستمر والمتردد

كما تعلم أن الجهد أو التيار في أنظمة التيار المستمر لا يغير اتجاهه أبدًا. يكاد يكون ثابتًا بالنسبة للزمن. ومن ثم فإن حساب القدرة أو الجهد أو التيار سهل للغاية.

مثلا لنفترض أن مصباح كهربائي متصل بمصدر تيار مستمر بجهد 12 فولت والتيار المار عبر الدائرة هو 3A. من هذه القيم، يمكننا بسهولة حساب القدرة التي يستهلكها المصباح عن طريق ضرب الجهد في التيار، حيث أن قيم كل من الجهد والتيار ثابته.
P = VI = 12 X 3 = 36 watt
وهذه هي القدرة التي يستهلكها المصباح في أي وقت.

الآن، إذا قمنا بتغيير مصدر التيار المستمر بمتردد. في هذه الحالة الجهد والتيار لم يعدا ثابتين. ستتغير قيمة الجهد والتيار الآن بشكل متواصل ولحظي. اننظر إلى شكل موجة الجهد المتردد التالية:

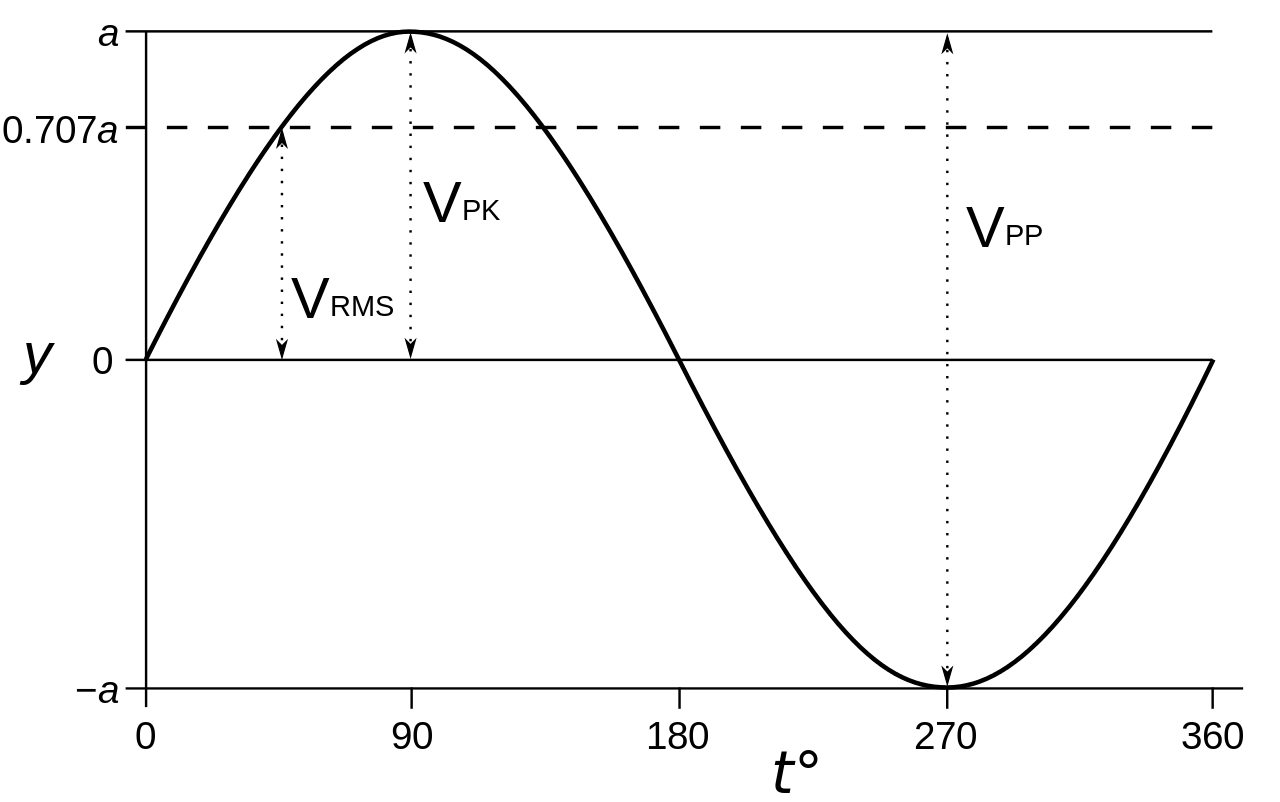
لنفترض أن قيمة جهد الذروة Vpeak=10V، في البداية، سيكون الجهد صفر، بعد فترة من الوقت سيصل إلى 5V، وبعد مرور بعض الوقت سوف يزداد إلى 10V. مرة أخرى بعد مرور بعض الوقت سوف تنخفض إلى 10V، 5V ،0V ،-5V ،-10V ،-5V وستستمر الدورة وتتكرر في الثانية الواحدة 60 أو 50 مره بحسب تردد الموجة.‌‌

إذًا كم قيمة الجهد؟ لو أخذنا في الإعتبار إما 5 فولت إلى -5 فولت أو 10 فولت إلى -10 فولت (peak to peak)  أو أي قيمة أخرى للجهد لحساب القدرة، فسيؤدي ذلك إلى نتيجة خاطئة. لأن القيمة تبقى صحيحة فقط لفترة زمنية معينة، وبعد ذلك الوقت تتغير القيمة.

تزداد الأمور سوءًا عند مقارنتها بأشكال موجية مختلفة. على سبيل المثال ، إذا كنا نقارن موجة جيبية مع موجة مربعة، فإن الموجة الجيبية سيكون ذروة قيمتها لفترة زمنية أصغر من الموجة المربعة‌‌.

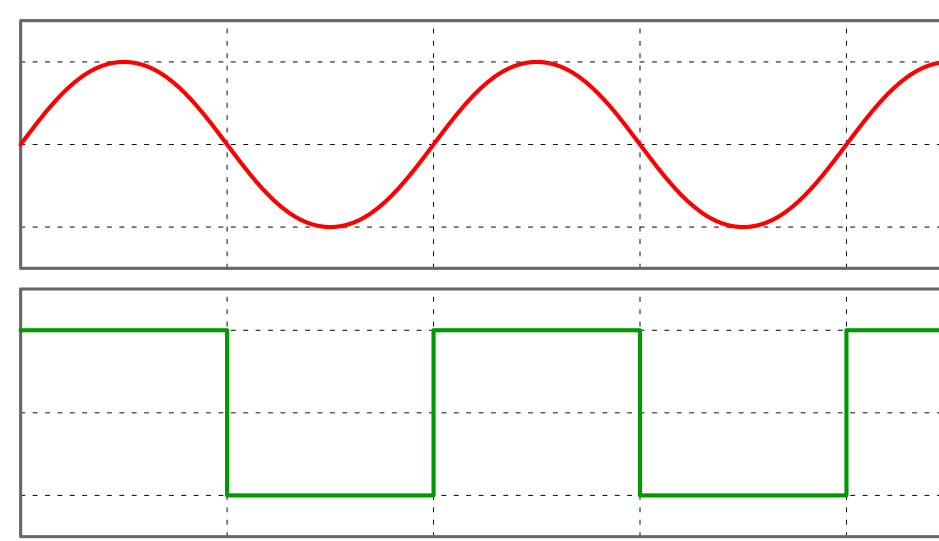
ومن ثم فإن تأثير الموجتين عندما يعملان على تشغيل نفس الحمل، سيكون مختلفًا. نستنتج من هذا أن اعتبار قيمة جهد peak to peak لإجراء العمليات الحسابية فكرة غير عملية.

لذا، نحن بحاجة إلى حل لهذا، نحتاج إلى مصطلح يعطينا القيمة الفعلية للتيار المتردد، نحتاج إلى مصطلح يمكننا التعامل معه لحساب القدرة والجهد والتيار المتردد والذي سيظل صحيحًا لمعظم الوقت.‌‌

لحسن الحظ ، لا داعي للقلق، فهناك طريقة لحساب القيمة الفعلية في دوائر التيار المتردد بإستخدام نظرية القيمة الفعالة.

ماهي القيمة الفعالة RMS Value؟

تُعرَّف القيمة الفعالة للتيار المتردد بأنها قيمة التيار المتردد الذي إذا مر في دائرة لفترة زمنية معينة فإنه يعطي نفس التأثير الحراري للتيار المستمر عندما يمر في نفس الدائرة لنفس الزمن. وهي القيمة التي نحصل عليها في أجهز القياس كالأميتر و الفولتميتر. وتسمى أيضًا (effective value).

على سبيل المثال إذا كان لديك بطارية 12 فولت تُضيء مصباح كهربائي بقدرة 24 واط بتيار مستمر. بالنسبة للتيار المتردد. فيجب أن تكون القيمة الفعالة RMS value تساوي 12 فولت. ليعطي نفس خرج القدرة 24 واط.

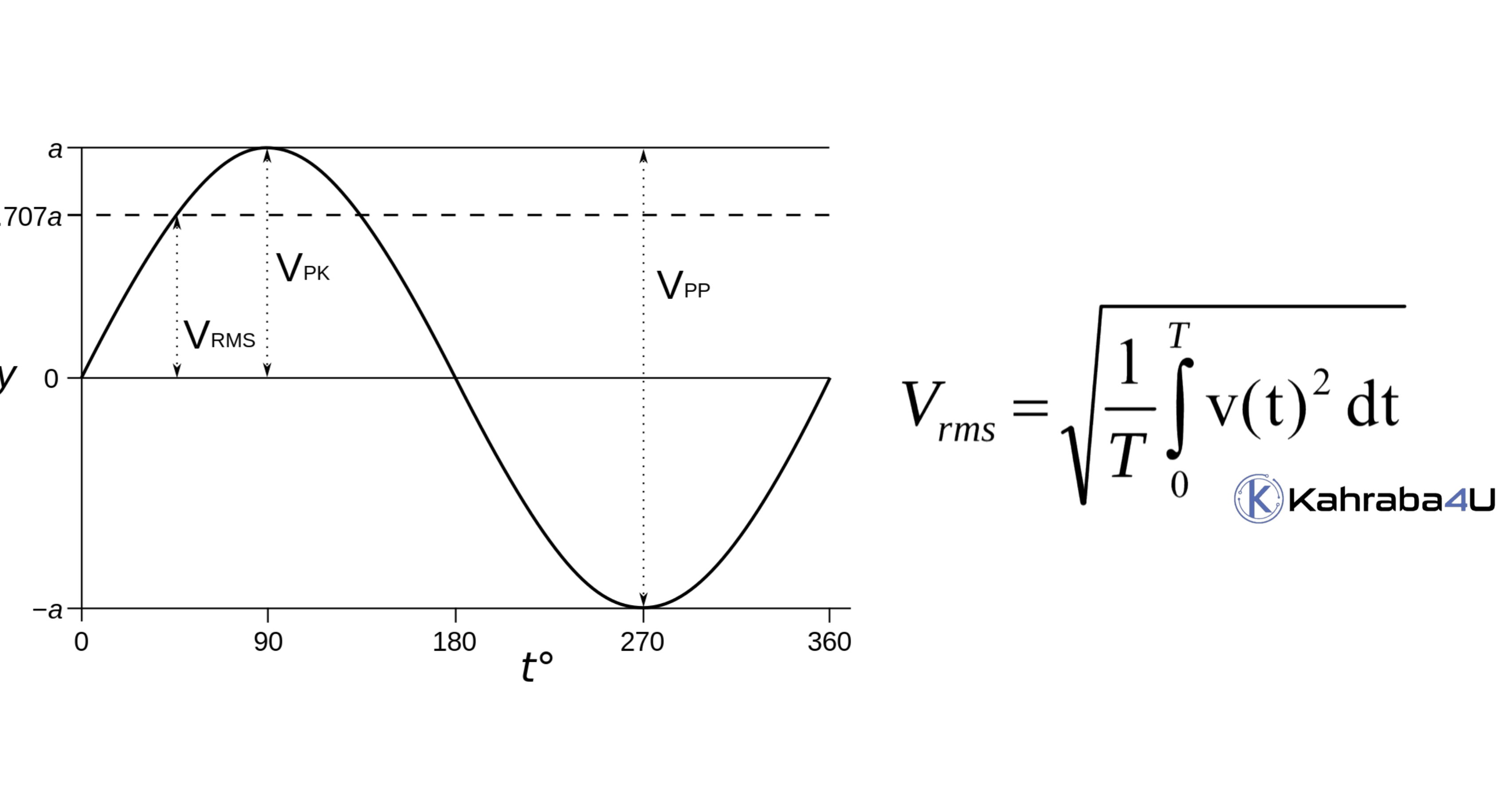
فكما هو واضح، تكون القيمة الفعالة للجهد RMS Voltage دائمًا أقل من القيمة القصوى peak value للجهد Vp. لأن القيمة القصوى تحدث مرتين فقط في الدورة الواحدة. في بقية الوقت من زمن الدورة الواحدة تكون قيمة الموجة أقل. ‏انظر للشكل 

في معظم دول العالم قيمة الجهد 220V وللحصول على هذه القيمة لابد ان تكون القيمة القصوى للجهد (220×1.41)=311 فولت .(لا تقلق. سأوضح من أين اتيت بهذا القانون لاحقًا).

طرق إيجاد القيمة الفعالة RMS

يمكن تحديد القيمة الفعالة للجهد RMS لشكل موجة جيبية أو معقد بطريقتين أساسيتين:

• طريقة الرسم البياني: والتي يمكن استخدامها للعثور على قيمة RMS لأي شكل موجة غير جيبية متغيرة بمرور الزمن عن طريق تقسيم الموجة لعدد من النقاط المتساوية، ويمكن استخدامها أيضا مع الموجة الجيبية.

• الطريقة الحسابية (الرياضية): هي عملية رياضية لإيجاد القيمة الفعالة أو قيمة RMS لأي جهد أو تيار ذي موجة دورية بإستخدام حساب التفاضل والتكامل.‌‌

1. طريقة الرسم البياني لإيجاد القيمة الفعالة RMS

يمكن إيجاد القيمة الفعالة للموجة بدقة جيدة عن طريق أخذ قيم لحظية متباعدة بشكل متساوٍ على طول الموجة.

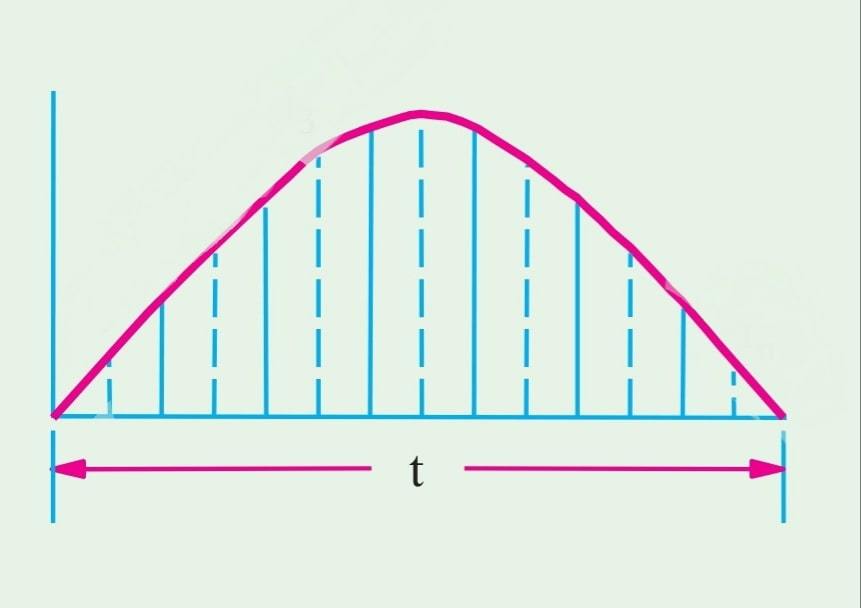
وبما أن طريقة الحساب هي نفسها لكلا نصفي موجة التيار المتردد، في هذا المثال سنأخذ الحسابات فقط لنصف الدورة الموجبة.

1- نقوم بتقسيم شكل الموجة لأقسام متساوية

يمكن إيجاد القيمة الفعالة للموجة بدقة جيدة عن طريق أخذ قيم لحظية متباعدة بشكل متساوٍ على طول شكل الموجة كما في الصورة السابقة.

يتم تقسيم النصف الموجب من الشكل الموجي إلى أي عدد من الأجزاء المتساوية “n” وكلما زادت عدد النقاط المأخوذه على طول شكل الموجة، كلما كانت النتيجة النهائية أكثر دقة.

2 – خذ مربع كل قيمة

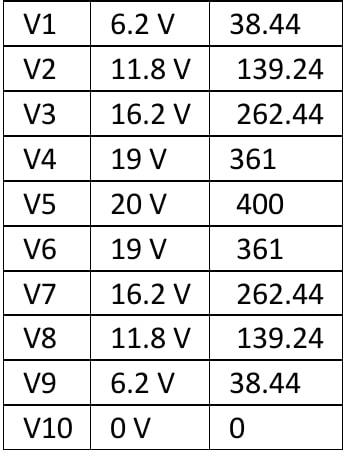
يتم ضرب كل قيمة إحداثية متوسطة للموجة بنفسها(تربيع القيمة) وتضاف إلى القيمة التالية. تعطينا هذه الطريقة الجزء “المربع” أو التربيعي من تعبير الجهد RMS.

3 – خذ متوسط القيم

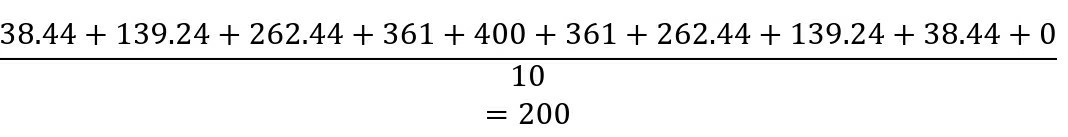
يتم جمع هذه القيمة التربيعية وقسمتها على عدد الإحداثيات المستخدمة وفي مثالنا البسيط أعلاه ، كان عدد القيم المستخدمة هو 10.

4 – أخذ الجذر التربيعي
أخيرًا خذ الجذر التربيعي للقيمة النهائية الناتجة من الخطوة الثالثة.

√200=14.14

ومن هذه الطريقة جاءت سبب تسميتها Root Mean Square Value بمعنى الجذر التربيعي لمتوسط مربع القيم المتساوية على طول الموجة.

2. إيجاد القيمة الفعالة للموجة الجيبية حسابيًا

الطريقة البيانية أعلاه هي طريقة جيدة جدًا لإيجاد القيمة الفعالةللجهد أو التيار لشكل موجة مترددة غير متماثلة أو غير جيبية بطبيعتها. بمعنى الموجة ذات الشكل المعقد، ولكن عند التعامل مع أشكال موجية جيبية نقية، يمكننا أن نجعل الأمر أسهل قليلاً على أنفسنا باستخدام طريقة تحليلية أو رياضية لإيجاد قيمة RMS.‌‌

قانون القيمة الفعالة للتيار المتردد

معادلة الموجة الجيبية تُعطى بالقانون التالي:

V(t) = V_max*sin(ωt)

قانون القيمة الفعالة للتيار المتردد RMS Value :

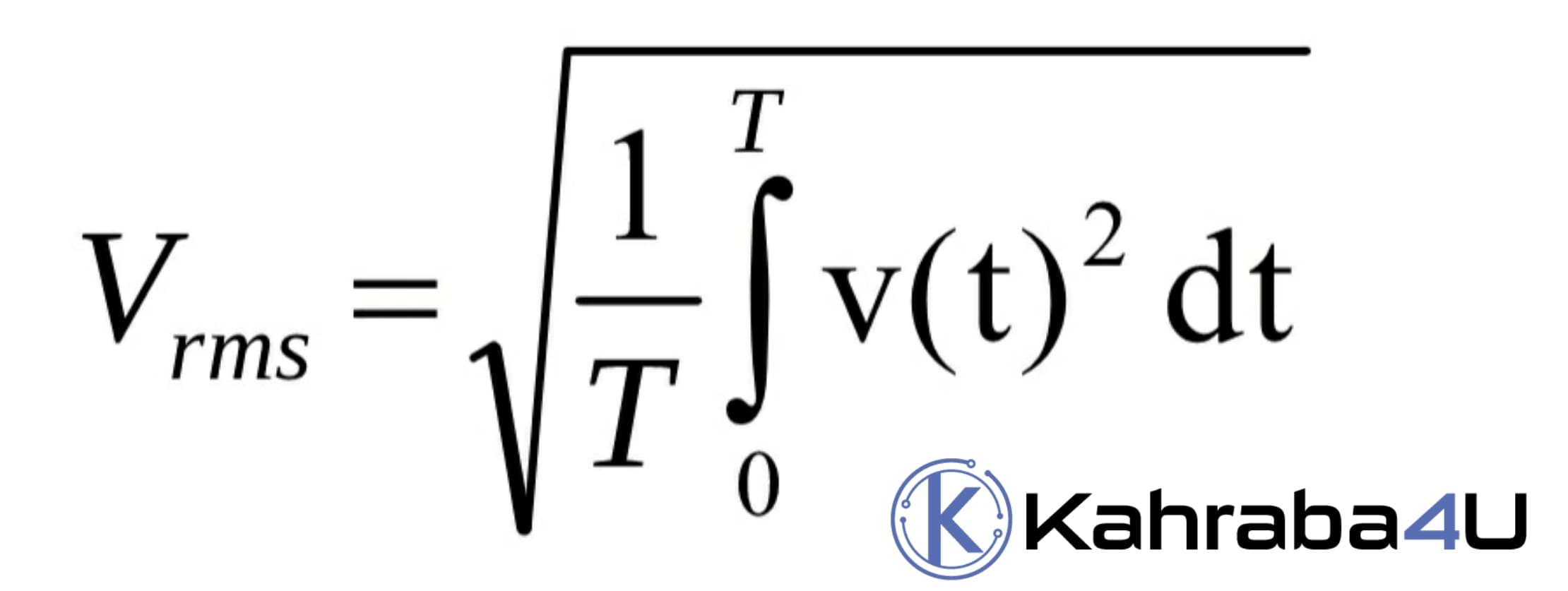
وبتكامل المعادلة السابقة للموجة الجيبية نحصل على التالي:

V_rms=0.707*V_max

وبتطبيق نفس المعادلة على التيار تكون القيمة الفعالة للتيار :

I_rms=0.707*I_max

مثال على إيجاد القيمة الفعالة للموجة الجيبية

إذا كانت قيمة الجهد تساوي V(t) = 30sin(377t) أوجد القيمة الفعالة للجهد RMS Value

الحل : بتطبيق المعادلة السابقة يمكن حساب قيمة RMS كالتالي:

V_rms = 0.707*V_max

= 0.707*30 = 21.21V

ملخص عن القيمة الفعالة RMS

• تقيس أجهزة القياس مثل الأميتر والملتيميتر والفولتميتر القيمة الفعالة باعتبار أن الموجة المقاسة جيبية.
• لقياس القيمة الفعالة للموجة غير الجيبية، يجب إستخدام أجهزة قياس دقيقة ومخصصة لهذا الغرض.
• يتم حساب قيمة RMS بإستخدام القانون (Vp*0.707) فقط للتيار المتردد و الجهد ذو الشكل الجيبي.
• حساب قيمة RMS للموجة غير الجيبية بإستخدام طريقة الرسم البياني
• لا يتم استخدام القيمة الفعالة مع التيار المستمر DC لأن التيار المستمر ثابت مع الزمن.

في هذه المقال تم شرح ما هي القيمة الفعالة للتيار المتردد بالتفصيل. مع شرح القوانين وتقديم مثال لإبجاد قيمتها. آمل أن يتم فهم كل نقطة بوضوح حول القيمة الفعالة. وطرق إيجادها.

‏إذا ما زلت غير قادر على فهم أي من المعلومات الواردة في المقال. أو هناك استفسار حول ماتم تقديمه. فلا تتردد في طرح سؤال في مربع التعليق أدناه. ‏