يتكون قانون كيرشوف من معادلتين نشرها غوستاف كيرشوف لأول مرة في عام 1845 واحدةتخص الجهد والأخرى يخص التيار،
ويعتبر قانون كيرشوف من أهم القوانين في الكهرباء وله تطبيقات ليس فقط على دوائر التيار المستمر ولكن أيضًا على دوائر التيار المتردد والدوائر الرقمية.
هذه القوانين واسعة التطبيقات ومفيدة جدًا في إيجاد حلول للدوائر التي تتركنا أحيانًا حائرين في كيفية حلها. وهذه القوانين لن تصبح قديمة ولن يتم استبدالها أو الاستغناء عنها.
قانون كيرشوف الأول للتيار
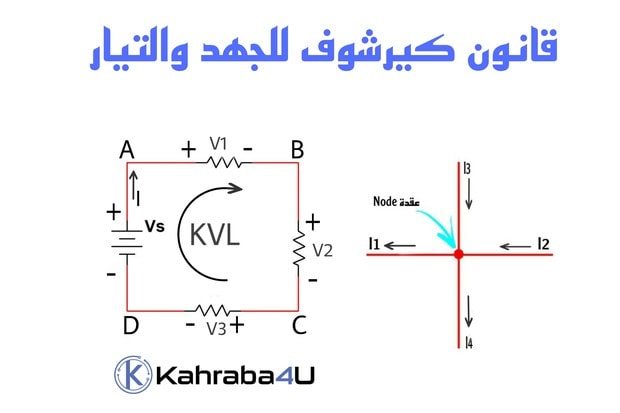
قانون كيرشوف الأول للتيار (Kirchhoff’s Current Law (KCL)) ينص على أن المجموع الجبري للتيارات الداخلة والخارجة من عقدة (نقطة) Node في الدائرة تساوي صفر، ويمكن إعادة صياغة القانون كما يلي: مجموع التيارات الداخلة لعقدة تساوي مجموع التيارات الخارجة من نفس العقدة .
ويمكن التعبير عن القانون بالمعادلة التالية:
∑Ii=∑Io
حيث أن ∑ تعني المجموع الجبري، و Ii تعني التيارات الداخلة للعقدة، و Io تعني التيارات الخارجة من العقدة.
انظر للدائرة في الصورة التالية:
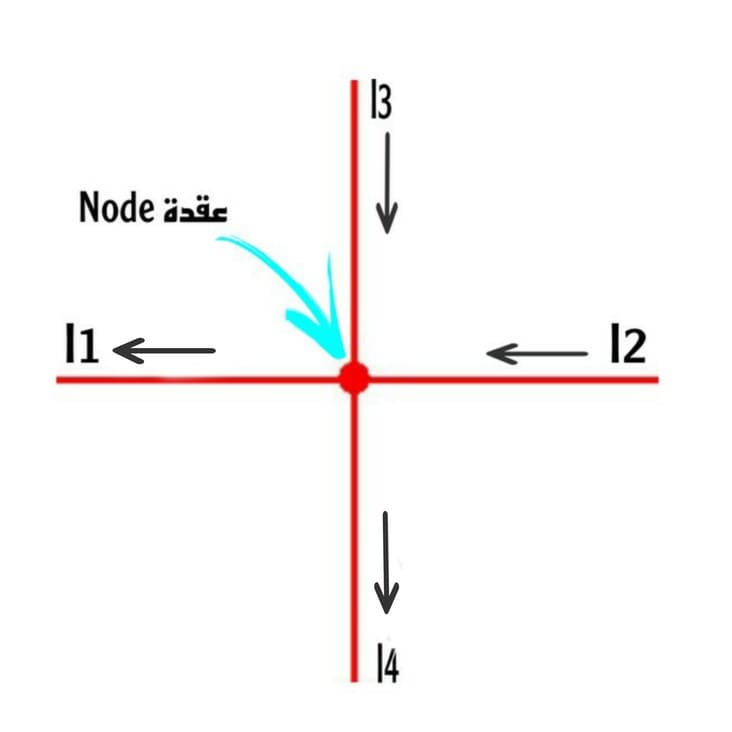
عند تطبيق قانون كيرشوف للتيار ستكون التيارات الداخلة للعقدة هي I3 و I2 بينما التيارات الخارجة منها هي I1 و I4
وبتطبيق قانون كيرشوف للتيار نحصل على المعادلة التالية: I1+I4=I2+I3
ومن هذه المعادلة يمكنك إيجاد أي تيار مجهول القيمة بمعرفة بقية القيم بسهولة.
مسائل على قانون كيرشوف للتيار
أوجد قيمة التيار الرابع I4 في الدائرة الموجودة في الصورة التالية:
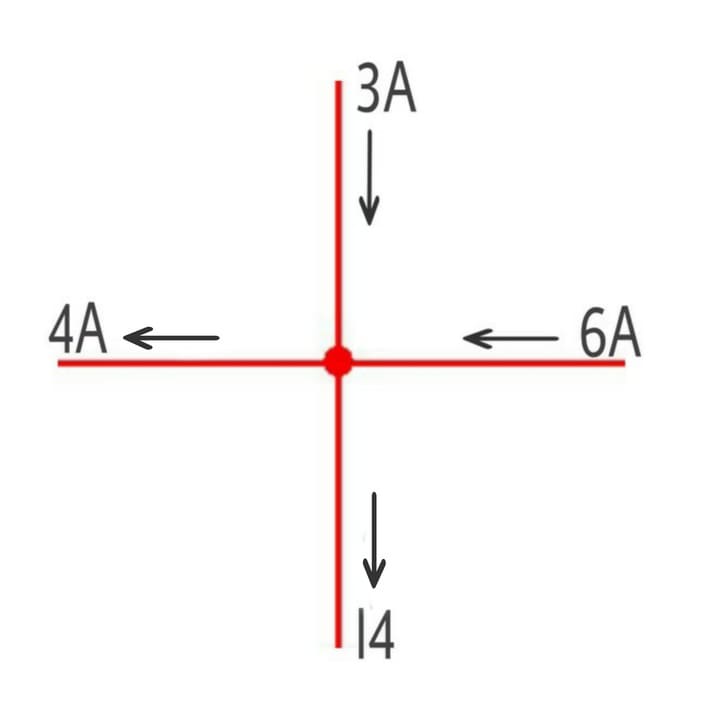
الحل:
باستخدام قانون كيرشوف الأول للتيار نحصل على المعادلة التالية: I4+4=6+3
بترتيب المعادلة: I4=6+3-4 ونحصل على: I4=5A.
قانون كيرشوف الثاني للجهد
ينص قانون كيرشوف الثاني للجهد (Kirchhoff’s Voltage Law (KVL)) على أن المجموع الجبري لكل الجهود في مسار مغلق يساوي صفر، ويمكن صياغته بطريقة أخرى وهي أن مجموع الجهود المفقودة في المسار المغلق يساوي جهد المصدر لهذا المسار.
ويتطلب تطبيق القانون أن نحدد مسارًا مغلقًا لنعمل عليه، مما يسمح لنا أن نبدأ في نقطة معينة في الدائرة والمرور بالمسار المغلق في الدائرة،والرجوع إلى نقطة البداية الأصلية. كما في الصورة التالية
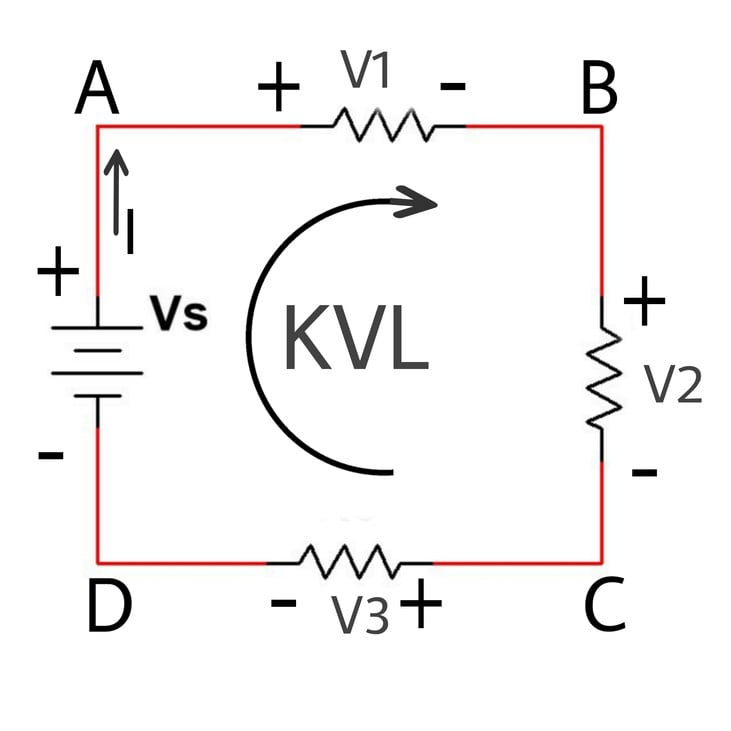
إذا بدأنا من النقطة A واتبعنا مسار التيار فسننتهي بنقطة B وبالاستمرار سنمر عبر النقطة C وD وأخيرًا سنعود عبر مصدر الجهد إلى النقطة A، نقطة البداية. إذن المسار ABCD يمثل مسار مغلق (أو حلقة مغلقة).
وينص القانون على أن مجموع الجهد خلال هذا المسار يساوي صفر ويمكن كتابة العلاقة الرياضية لهذا القانون كما يلي:
∑v=0
حيث ∑ تعني المجموع الجبري، والحرف v يرمز للجهود الكلية في المسار المغلق. ويجب مراعاة الإشارات عند الجمع.
وقد تتساءل في أي اتجاه يجب أن أتحرك في المسار المغلق؟ هل مع عقارب الساعة أو عكسها؟ وهل يجب أن اتبع مسار التيار دائمًا؟ والإجابة باختصار أن الإتجاه غير مهم وبإمكانك ان تفترض الإتجاه كما تريد مع الانتباه للإشارات، ولكن في الغالب يتم اخذ اتجاه عقارب الساعة.
قد يتبادر لذهنك سؤال آخر هو كيف أضع إشارة على الفولتية المختلفة وأنا أتحرك في اتجاه عقارب الساعة؟ قم بوضع إشارة موجبة عند الإنتقال من السالب إلى الموجب، وضع إشارة سالبة عند الإنتقال من الموجيب إلى السالب.
في الصورة السابقة، مثلًا عندما ننتقل من النقطة d إلى النقطة a عبر مصدر الجهد ، ننتقل من سالب إلى موجب لذلك نضع إشارة موجبة لجهد المصدر. وعندما تتحرك من النقطة a إلى النقطة b، تجد إشارة موجبة تليها إشارة سالبة، لذلك نضع إشارة سالبة. ونكمل بنفس الطريقة مع بقية المقاومات. وفي النهاية نحصل على المعادلة التالية:
+VS-V1-V2-V3=0
ويمكن إعادة كتابتها كما يلي
VS=V1+V2+V3
مسائل على قانون كيرشوف الثاني للجهد
أوجد قيمة الجهد V2 في الدائرة التالية:
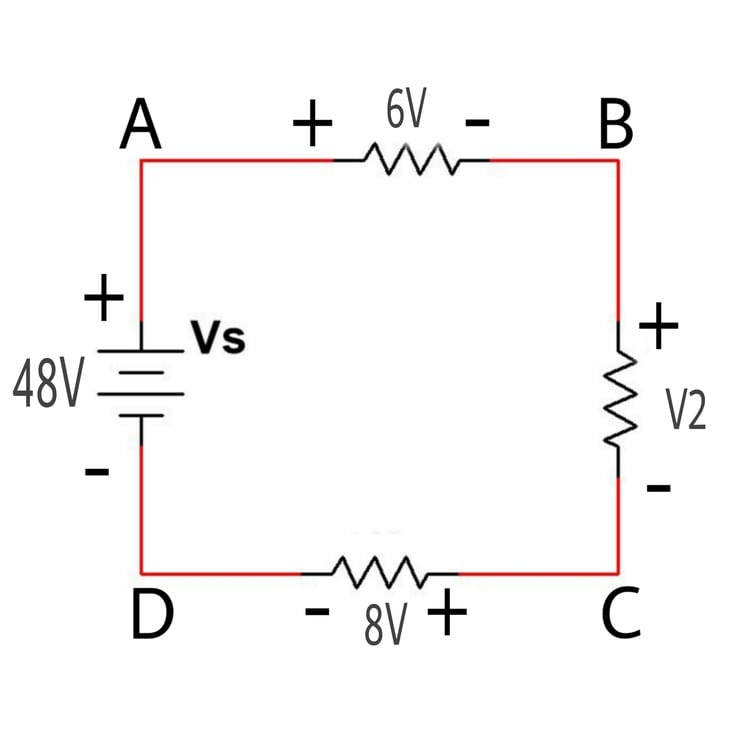
الحل: باستخدام قانون كيرشوف للجهد نحصل على المعادلة التالية:
+48-6-V2-8=0
باعادة ترتيب المعادلة:
V2=48-6-8
V2=34V
المصادر
Robert L. Boylestad, INTRODUCTORY CIRCUIT ANALYSIS




زين ….. شكرا علي المعلومات الجيدة
نرغب شرح كتاب ….الكهربائية المغناطسية